Gibanje telesa navzgor po nagnjeni ravnini. Nagnjena ravnina. Opis laboratorijske postavitve
V. M. Zraževskega
LABORATORIJSKO DELO ŠT.
KOTALJANJE TRDNEGA TELESA Z NAGNJENE RAVNINE
Cilj dela: Preverjanje zakona o ohranitvi mehanske energije pri kotaljenju togega telesa po nagnjeni ravnini.
Oprema: nagnjena ravnina, elektronska štoparica, valji različnih mas.
Teoretične informacije
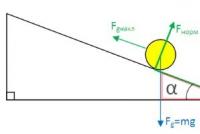
Naj ima valj polmer R in masa m se kotali po nagnjeni ravnini, ki s horizontom tvori kot α (slika 1). Na valj delujejo tri sile: gravitacija p = mg, sila normalnega pritiska ravnine na valj N in sila trenja valja na ravnini F tr. , ki leži v tej ravnini.
Cilinder je hkrati udeležen v dveh vrstah gibanja: translacijskem gibanju središča mase O in rotacijskem gibanju glede na os, ki poteka skozi središče mase.
Ker valj med gibanjem ostane na ravnini, je pospešek središča mase v smeri normale na nagnjeno ravnino enak nič, torej
p∙cosα − N = 0. (1)
Enačba za dinamiko translacijskega gibanja vzdolž nagnjene ravnine je določena s silo trenja F tr. in gravitacijsko komponento vzdolž nagnjene ravnine mg∙sinα:
ma = mg∙sinα − F tr. , (2)
Kje a– pospešek težišča valja vzdolž nagnjene ravnine.
Enačba za dinamiko rotacijskega gibanja glede na os, ki poteka skozi središče mase, ima obliko
jazε = F tr. R, (3)
Kje jaz– vztrajnostni moment, ε – kotni pospešek. Gravitacijski moment in  glede na to os je nič.
glede na to os je nič.
Enačbi (2) in (3) veljata vedno, ne glede na to, ali se valj giblje po ravnini z drsenjem ali brez drsenja. Toda iz teh enačb je nemogoče določiti tri neznane količine: F tr. , a in ε je potreben še en dodaten pogoj.
Če je sila trenja dovolj velika, se valj kotali po nagnjeni poti brez zdrsa. Nato morajo točke na obodu valja prepotovati enako dolžino kot središče mase valja. V tem primeru linearni pospešek a in kotni pospešek ε sta povezana z razmerjem
a = Rε. (4)
Iz enačbe (4) je ε = a/R. Po zamenjavi v (3) dobimo
 .
(5)
.
(5)
Zamenjava v (2) F tr. na (5), dobimo
 .
(6)
.
(6)
Iz zadnje relacije določimo linearni pospešek
 .
(7)
.
(7)
Iz enačb (5) in (7) je mogoče izračunati silo trenja:
 .
(8)
.
(8)
Sila trenja je odvisna od kota naklona α, gravitacije p = mg in od odnosa jaz/gospod 2. Brez trenja ne bo kotaljenja.
Pri kotaljenju brez drsenja igra vlogo sila statičnega trenja. Sila kotalnega trenja ima tako kot sila statičnega trenja največjo vrednost, ki je enaka μ N. Potem bodo pogoji za kotaljenje brez drsenja izpolnjeni, če
F tr. ≤ μ N. (9)
Ob upoštevanju (1) in (8) dobimo
 ,
(10)
,
(10)
ali končno
 .
(11)
.
(11)
V splošnem primeru lahko vztrajnostni moment homogenih simetričnih vrtilnih teles okoli osi, ki poteka skozi središče mase, zapišemo kot
jaz = kmR 2 , (12)
Kje k= 0,5 za poln valj (disk); k= 1 za votel tankostenski valj (obroč); k= 0,4 za trdno kroglo.
Po zamenjavi (12) v (11) dobimo končni kriterij, da se togo telo kotali z nagnjene ravnine brez zdrsa:
 .
(13)
.
(13)
Ker je pri kotaljenju trdnega telesa po trdni podlagi sila kotalnega trenja majhna, je skupna mehanska energija kotalnega telesa konstantna. V začetnem trenutku, ko je telo na zgornji točki nagnjene ravnine na višini h, je njegova skupna mehanska energija enaka potencialni:
W n = mgh = mg∙sinα, (14)
Kje s– pot, ki jo opravi središče mase.
Kinetično energijo kotalečega se telesa sestavlja kinetična energija translacijskega gibanja središča mase s hitrostjo υ in rotacijsko gibanje s hitrostjo ω glede na os, ki poteka skozi središče mase:
 .
(15)
.
(15)
Pri kotaljenju brez drsenja sta linearna in kotna hitrost povezani z razmerjem
υ = Rω. (16)
Pretvorimo izraz za kinetično energijo (15) tako, da vanj nadomestimo (16) in (12):
Gibanje po nagnjeni ravnini je enakomerno pospešeno:
 .
(18)
.
(18)
Transformirajmo (18) ob upoštevanju (4):
 .
(19)
.
(19)
Če skupaj rešimo (17) in (19), dobimo končni izraz za kinetično energijo telesa, ki se kotali po nagnjeni ravnini:
 .
(20)
.
(20)
Opis namestitve in merilne metode
Kotaljenje telesa po nagnjeni ravnini lahko preučujete z enoto "ravnina" in elektronsko štoparico SE1, ki sta del modularnega izobraževalnega kompleksa MUK-M2.
U  Namestitev je nagnjena ravnina 1, ki jo je mogoče namestiti pod različnimi koti α glede na obzorje s pomočjo vijaka 2 (slika 2). Kot α merimo s skalo 3. Valj 4 z maso m. Predvidena je uporaba dveh valjev različnih tež. Valji so pritrjeni na zgornji točki nagnjene ravnine z elektromagnetom 5, ki se krmili z
Namestitev je nagnjena ravnina 1, ki jo je mogoče namestiti pod različnimi koti α glede na obzorje s pomočjo vijaka 2 (slika 2). Kot α merimo s skalo 3. Valj 4 z maso m. Predvidena je uporaba dveh valjev različnih tež. Valji so pritrjeni na zgornji točki nagnjene ravnine z elektromagnetom 5, ki se krmili z
elektronska štoparica SE1. Razdalja, ki jo prepotuje valj, se meri z ravnilom 6, pritrjenim vzdolž ravnine. Čas kotaljenja valja se samodejno meri s senzorjem 7, ki izklopi štoparico v trenutku, ko se valj dotakne končne točke.
Delovni nalog
1. Odvijte vijak 2 (slika 2), nastavite ravnino pod določenim kotom α glede na vodoravno ravnino. Postavite valj 4 na nagnjeno ravnino.
2. Preklopno stikalo za krmiljenje elektromagnetov mehanske enote preklopite v položaj "ravno".
3. Štoparico SE1 nastavite na način 1.
4. Pritisnite gumb za zagon štoparice. Izmerite čas valjanja.
5. Poskus ponovimo petkrat. Rezultate meritev zapišite v tabelo. 1.
6. Izračunajte vrednost mehanske energije pred in po valjanju. Potegnite zaključek.
7. Ponovite korake 1-6 za druge kote naklona ravnine.
Tabela 1
|
t jaz, c |
(t jaz − <t>) 2 |
načine s, m |
Kot nagiba |
valj, kg |
W p, j |
W K, J |
|
|
t(a, n) |
<t> |
å( t jaz – <t>) 2 |
Δ s, m |
Δ m, kg |
|||
8. Ponovite korake 1-7 za drugi video. Rezultate zapišite v tabelo. 2, podobno tabeli. 1.
9. Pripravite zaključke na podlagi vseh rezultatov dela.
Kontrolna vprašanja
1. Poimenujte vrste sil v mehaniki.
2. Pojasnite fizikalno naravo sil trenja.
3. Kaj je koeficient trenja? Njegova velikost?
4. Kateri dejavniki vplivajo na koeficient statičnega, drsnega in kotalnega trenja?
5. Opišite splošno naravo gibanja togega telesa med kotaljenjem.
6. Kakšna je smer tornega momenta pri kotaljenju po nagnjeni ravnini?
7. Zapišite sistem enačb dinamike, ko se valj (krogla) kotali po nagnjeni ravnini.
8. Izpelji formulo (13).
9. Izpelji formulo (20).
10. Krogla in valj z enakima masama m in enakih radijev R istočasno začnite drseti po nagnjeni ravnini z višine h. Ali bodo hkrati dosegli spodnjo točko ( h = 0)?
11. Pojasnite razlog za zaviranje kotalečega se telesa.
Bibliografija
1. Savelyev, I. V. Tečaj splošne fizike v 3 zvezkih T. 1 / I. V. Savelyev. – M.: Nauka, 1989. – § 41–43.
2. Khaikin, S. E. Fizikalne osnove mehanike / S. E. Khaikin. – M: Nauka, 1971. – § 97.
3. Trofimova T. I. Tečaj fizike / T. I. Trofimova. – M: Višje. šola, 1990. – § 16–19.
Na površju Zemlje gravitacija (gravitacija) je konstantna in enaka produktu mase padajočega telesa in gravitacijskega pospeška: F g = mg
Upoštevati je treba, da je pospešek prostega pada konstantna vrednost: g=9,8 m/s 2 in je usmerjen proti središču Zemlje. Na podlagi tega lahko rečemo, da bodo telesa z različnimi masami padla na Zemljo enako hitro. Kako to? Če z iste višine vržete kos vate in opeko, se bo slednja hitreje prebila na tla. Ne pozabite na zračni upor! Za vato bo pomembno, saj je njena gostota zelo nizka. V brezzračnem prostoru bosta opeka in volna padli hkrati.
Žoga se giblje po nagnjeni ravnini, dolgi 10 metrov, naklonski kot ravnine je 30°. Kakšna bo hitrost žogice na koncu ravnine?
Na kroglico deluje samo gravitacijska sila Fg, usmerjena navzdol pravokotno na osnovo ravnine. Pod vplivom te sile (komponenta, usmerjena vzdolž površine ravnine) se bo žoga premaknila. Kakšna bo komponenta gravitacije, ki deluje vzdolž nagnjene ravnine?
Za določitev komponente je potrebno poznati kot med vektorjem sile F g in nagnjeno ravnino.
Določanje kota je precej preprosto:
- vsota kotov katerega koli trikotnika je 180°;
- kot med vektorjem sile F g in vznožjem nagnjene ravnine je 90°;
- kot med nagnjeno ravnino in njeno osnovo je α
Glede na zgoraj navedeno bo želeni kot enak: 180° - 90° - α = 90° - α
Iz trigonometrije:
Fg naklon = Fg cos(90°-α)
Sinα = cos(90°-α)
F g naklon = F g sinα
Res je tako:
- pri α=90° (navpična ravnina) F g nagib = F g
- pri α=0° (vodoravna ravnina) F g nagib = 0
Določimo pospešek žoge po dobro znani formuli:
F g sinα = m a
A = F g sinα/m
A = m g sinα/m = g sinα
Pospešek žogice vzdolž nagnjene ravnine ni odvisen od mase žogice, temveč le od naklonskega kota ravnine.
Določite hitrost žogice na koncu ravnine:
V 1 2 - V 0 2 = 2 a s
(V 0 =0) - žoga se začne premikati z mesta
V 1 2 = √2·a·s
V = 2 g sinα S = √2 9,8 0,5 10 = √98 = 10 m/s
Bodite pozorni na formulo! Hitrost telesa na koncu nagnjene ravnine bo odvisna le od kota naklona ravnine in njene dolžine.
V našem primeru bodo imeli biljardna krogla, osebni avtomobil, tovornjak in šolar na saneh na koncu ravnine hitrost 10 m/s. Trenj seveda ne upoštevamo.
Telo, ki drsi po nagnjeni ravnini. V tem primeru nanj delujejo naslednje sile:
Gravitacija mg usmerjena navpično navzdol;
Podporna reakcijska sila N, usmerjena pravokotno na ravnino;
Sila drsnega trenja Ftr je usmerjena nasprotno od hitrosti (navzgor po nagnjeni ravnini, ko telo drsi).
Vstavimo nagnjeni koordinatni sistem, katerega os OX je usmerjena navzdol vzdolž ravnine. To je priročno, saj boste v tem primeru morali razstaviti samo en vektor na komponente - gravitacijski vektor mg, vektorja sile trenja Ftr in podporne reakcijske sile N pa sta že usmerjena vzdolž osi. Pri tej ekspanziji je x-komponenta gravitacijske sile enaka mg sin(α) in ustreza "vlečni sili", ki je odgovorna za pospešeno gibanje navzdol, y-komponenta - mg cos(α) = N pa uravnoteži podporna reakcijska sila, ker se telo premika vzdolž osi OY odsotno.
Sila drsnega trenja Ftr = µN je sorazmerna sili reakcije nosilca. To nam omogoča, da dobimo naslednji izraz za silo trenja: Ftr = µmg cos(α). Ta sila je nasprotna "vleče" komponenti gravitacije. Zato za telo, ki drsi navzdol, dobimo izraze za skupno rezultanto sile in pospešek:
Fx = mg(sin(α) – µ cos(α));
ax = g(sin(α) – µ cos(α)).
pospešek:
hitrost je
v=ax*t=t*g(sin(α) – µ cos(α))
po t=0,2 s
hitrost je
v=0,2*9,8(sin(45)-0,4*cos(45))=0,83 m/s
Silo, s katero telo privlači Zemljo pod vplivom gravitacijskega polja Zemlje, imenujemo gravitacija. Po zakonu univerzalne gravitacije na površje Zemlje (ali blizu tega površja) na telo z maso m deluje sila težnosti.
Ft=GMm/R2 (2,28)
kjer je M masa Zemlje; R je polmer Zemlje.
Če na telo deluje le sila težnosti, vse druge sile pa so medsebojno uravnotežene, telo prosto pada. V skladu z drugim Newtonovim zakonom in formulo (2.28) se modul gravitacijskega pospeška g izračuna po formuli
g=Ft/m=GM/R2. (2,29)
Iz formule (2.29) sledi, da pospešek prostega pada ni odvisen od mase m padajočega telesa, tj. za vsa telesa na določenem mestu na Zemlji je enaka. Iz formule (2.29) sledi Ft = mg. V vektorski obliki
V § 5 je bilo ugotovljeno, da ker Zemlja ni krogla, ampak krožni elipsoid, je njen polarni polmer manjši od ekvatorialnega. Iz formule (2.28) je razvidno, da je zaradi tega gravitacijska sila in gravitacijski pospešek, ki ga povzroča, na polu večja kot na ekvatorju.
Sila težnosti deluje na vsa telesa, ki se nahajajo v gravitacijskem polju Zemlje, vendar ne padejo vsa telesa na Zemljo. To je razloženo z dejstvom, da gibanje številnih teles ovirajo druga telesa, na primer nosilci, obešalne niti itd. Telesa, ki omejujejo gibanje drugih teles, imenujemo povezave. Pod vplivom gravitacije se vezi deformirajo in reakcijska sila deformirane povezave po tretjem Newtonovem zakonu uravnoteži silo gravitacije.
V § 5 je bilo tudi ugotovljeno, da na pospešek prostega pada vpliva vrtenje Zemlje. Ta vpliv je razložen na naslednji način. Referenčni sistemi, povezani z zemeljskim površjem (razen dveh, povezanih z zemeljskima poloma), strogo gledano niso inercialni referenčni sistemi – Zemlja se vrti okoli svoje osi, skupaj z njo pa se takšni referenčni sistemi gibljejo v krožnici s centripetalnim pospeškom. Ta neinercialnost referenčnih sistemov se kaže zlasti v tem, da se vrednost gravitacijskega pospeška na različnih mestih na Zemlji izkaže za različno in je odvisna od geografske širine kraja, kjer je referenčni sistem povezan z se nahaja Zemlja, glede na katero je določen gravitacijski pospešek.
Meritve, izvedene na različnih zemljepisnih širinah, so pokazale, da se številčne vrednosti gravitacijskega pospeška med seboj malo razlikujejo. Zato lahko z ne preveč natančnimi izračuni zanemarimo neinercialnost referenčnih sistemov, povezanih z zemeljsko površino, kot tudi razliko v obliki Zemlje od sferične in predpostavimo, da je gravitacijski pospešek kjerkoli na Zemlji enaka in enaka 9,8 m/s2.
Iz zakona univerzalne gravitacije sledi, da se gravitacijska sila in gravitacijski pospešek, ki ga povzroča, zmanjšujeta z večanjem oddaljenosti od Zemlje. Na višini h od zemeljske površine je modul gravitacijskega pospeška določen s formulo
Ugotovljeno je bilo, da je na višini 300 km nad zemeljskim površjem gravitacijski pospešek za 1 m/s2 manjši kot na zemeljskem površju.
Posledično se v bližini Zemlje (do višine nekaj kilometrov) gravitacijska sila praktično ne spremeni, zato je prosti pad teles v bližini Zemlje enakomerno pospešeno gibanje.
Telesna teža. Breztežnost in preobremenjenost
Silo, s katero telo zaradi privlačnosti na Zemljo deluje na svojo oporo ali obes, imenujemo teža telesa. Za razliko od gravitacije, ki je gravitacijska sila, ki deluje na telo, je teža elastična sila, ki deluje na oporo ali vzmetenje (tj. člen).
Opazovanja kažejo, da je teža telesa P, določena na vzmetni tehtnici, enaka sili težnosti Ft, ki deluje na telo le, če tehtnica s telesom glede na Zemljo miruje ali se giblje enakomerno in premočrtno; V tem primeru
Če se telo giblje pospešeno, je njegova teža odvisna od vrednosti tega pospeška in od njegove smeri glede na smer težnega pospeška.
Ko telo obesimo na vzmetno tehtnico, delujeta nanj dve sili: sila težnosti Ft=mg in prožnostna sila Fyp vzmeti. Če se v tem primeru telo giblje navpično navzgor ali navzdol glede na smer gravitacijskega pospeška, potem daje vektorska vsota sil Ft in Fup rezultanto, ki povzroči pospešek telesa, tj.
Fт + Fуп=ma.
Glede na zgornjo definicijo pojma "teža" lahko zapišemo, da je P = -Fyп. ob upoštevanju dejstva, da je Ft=mg, sledi mg-ma=-Fyп. Zato je P=m(g-a).
Sili Fт in Fуп sta usmerjeni vzdolž ene navpične ravne črte. Če je torej pospešek telesa a usmerjen navzdol (tj. sovpada v smeri s pospeškom prostega pada g), potem v modulu
Če je pospešek telesa usmerjen navzgor (tj. nasproti smeri pospeška prostega pada), potem
P = m = m(g+a).
Posledično je teža telesa, katerega pospešek po smeri sovpada s pospeškom prostega pada, manjša od teže mirujočega telesa, teža telesa, katerega pospešek je nasproten smeri pospeška prostega pada, pa večja. kot teža telesa v mirovanju. Povečanje telesne teže zaradi njegovega pospešenega gibanja imenujemo preobremenitev.
Pri prostem padu a=g. sledi, da je v tem primeru P = 0, kar pomeni, da uteži ni. Če se torej telesa gibljejo le pod vplivom gravitacije (tj. prosto padajo), so v breztežnostnem stanju. Značilnost tega stanja je odsotnost deformacij in notranjih napetosti v prosto padajočih telesih, ki jih povzroča gravitacija v mirovanju. Razlog za breztežnost teles je v tem, da daje sila težnosti prosto padajočemu telesu in njegovemu nosilcu (ali obesu) enake pospeške.
Naj bo majhno telo na nagnjeni ravnini z naklonskim kotom a (slika 14.3, A). Ugotovimo: 1) kolikšna je sila trenja, če telo drsi po nagnjeni ravnini; 2) kolikšna je sila trenja, če telo leži nepremično; 3) pri kateri najmanjši vrednosti naklonskega kota a začne telo drseti z nagnjene ravnine.
A) b) 
Sila trenja bo ovirati gibanje, zato bo usmerjeno navzgor vzdolž nagnjene ravnine (slika 14.3, b). Na telo poleg sile trenja delujeta še sila težnosti in normalna reakcijska sila. Predstavimo koordinatni sistem HOU, kot je prikazano na sliki, in poiščite projekcije vseh teh sil na koordinatne osi:
X: F tr X = –F tr, N X = 0, mg X = mg sina;
Y:F tr Y = 0, NY=N, mg Y = –mg cosa.
Ker lahko telo pospeši le vzdolž nagnjene ravnine, torej vzdolž osi X, potem je očitno, da je projekcija vektorja pospeška na os Y bo vedno nič: in Y= 0, kar pomeni vsoto projekcij vseh sil na os Y mora biti tudi nič:
F tr Y + N Y + mg Y= 0 Þ 0 + N–mg cosa = 0 Þ
N = mg cosa. (14,4)
Potem je sila drsnega trenja po formuli (14.3) enaka:
F tr.sk = m N= m mg cosa. (14,5)
Če telo počiva, potem vsota projekcij vseh sil, ki delujejo na telo, na os X mora biti enako nič:
F tr X + N X + mg X= 0 Þ – F tr + 0 +mg sina = 0 Þ
F tr.p = mg sina. (14,6)
Če postopoma povečujemo kot naklona, potem vrednost mg sina se bo postopoma povečevala, kar pomeni, da bo naraščala tudi sila statičnega trenja, ki se vedno »samodejno prilagaja« zunanjim vplivom in jih kompenzira.
Toda, kot vemo, "možnosti" sile statičnega trenja niso neomejene. Pri nekem kotu a 0 bo celoten "vir" sile statičnega trenja izčrpan: dosegla bo največjo vrednost, ki je enaka sili drsnega trenja. Potem bo enakost resnična:
F tr.sk = mg sina 0 .
Če v to enakost nadomestimo vrednost F tr.sk iz formule (14.5) dobimo: m mg cosa 0 = mg sina 0 .
Obe strani zadnje enakosti delimo z mg cosa 0, dobimo:
![]() Þ
Þ ![]() a 0 = arctgm.
a 0 = arctgm.
Torej je kot a, pod katerim telo začne drseti vzdolž nagnjene ravnine, podan s formulo:
a 0 = arctgm. (14,7)
Upoštevajte, da če je a = a 0, potem lahko telo nepremično leži (če se ga ne dotaknete) ali drsi s konstantno hitrostjo po nagnjeni ravnini (če ga malo potisnete). Če< a 0 , то тело «стабильно» неподвижно, и легкий толчок не произведет на него никакого «впечатления». А если a >a 0, potem bo telo zdrsnilo z nagnjene ravnine pospešeno in brez sunkov.
Problem 14.1.Človek nosi dve medsebojno povezani sani (slika 14.4, A), z uporabo sile F pod kotom a na vodoravno ravnino. Masi sani sta enaki in enaki T. Koeficient trenja tekačev na snegu m. Poiščite pospešek sani in natezno silo T vrvi med sani, pa tudi sila F 1, s katerim mora človek vleči vrv, da se sani enakomerno premikajo.
| F a m m |
 A) A)
|  b) riž. 14.4 b) riž. 14.4 |
| A = ? T = ? F 1 = ? |
rešitev. Zapišimo drugi Newtonov zakon za vsako sani v projekcijah na os X in pri(Sl. 14.4, b):
jaz pri: N 1 + F sina – mg = 0, (1)
x: F cosa - T–m N 1 = ma; (2)
II pri: N 2 – mg = 0, (3)
x: T–m N 2 = ma. (4)
Iz (1) najdemo N 1 = mg–F sina, iz (3) in (4) najdemo T = m mg+ + ma. Zamenjava teh vrednosti N 1 in T v (2), dobimo
![]() .
.
Nadomeščanje A v (4), dobimo
T= m N 2 + ma= m mg + to =
M mg + T ![]()
![]() .
.
Najti F 1, enačimo izraz za A na nulo:
Odgovori: ![]() ;
; ![]() ;
;
![]() .
.
STOP! Odločite se sami: B1, B6, C3.
Problem 14.2. Dve telesi z masama T in M vezan z nitjo, kot je prikazano na sl. 14,5, A. S kolikšnim pospeškom se telo giblje? M, če je koeficient trenja na površini mize m. Kakšna je napetost niti T? Kakšna je sila pritiska na os bloka?
| T M m | rešitev. Zapišimo Newtonov drugi zakon v projekcijah na os X 1 in X 2 (slika 14.5, b), glede na to: X 1: T - m Mg = Ma, (1) X 2: mg – T = ma. (2) Z reševanjem sistema enačb (1) in (2) ugotovimo: |
| A = ? T = ? R = ? |
Če se bremena ne premikajo, potem.
Odgovori: 1) če T < mM, To A = 0, T = mg, ; 2) če T³m M, to , ![]() ,
, ![]() .
.
STOP! Odločite se sami: B9–B11, C5.
Problem 15.3. Dve telesi z masama T 1 in T 2 sta povezana z nitjo, vrženo čez blok (slika 14.6). Telo T 1 je na nagnjeni ravnini z naklonskim kotom a. Koeficient trenja okoli ravnine m. Telesna masa T 2 visi na nitki. Poiščite pospešek teles, natezno silo niti in silo pritiska bloka na os pod pogojem, da T 2 < T 1. Upoštevajte tga > m.
riž. 14.7 
Zapišimo Newtonov drugi zakon v projekcijah na os X 1 in X 2, glede na to in:
X 1: T 1 g sina – T - m m 1 g cosa = m 1 a,
X 2: T–m 2 g = m 2 a.
![]() , .
, .
Ker A>0, torej
Če neenakost (1) ni izpolnjena, potem obremenitev T 2 zagotovo ne napreduje! Nato sta možni še dve možnosti: 1) sistem je negiben; 2) tovor T 2 se premakne navzdol (in breme T 1 oziroma navzgor).
Predpostavimo, da je obremenitev T 2 se premakne navzdol (slika 14.8).
riž. 14.8 
Nato enačbe drugega Newtonovega zakona na osi X 1 in X 2 bo videti takole:
X 1: T – t 1 g sina – m m 1 g cosa = m 1 a,
X 2: m 2 g – T = m 2 a.
Če rešimo ta sistem enačb, ugotovimo:
![]() , .
, .
Ker A>0, torej
 Torej, če je neenakost (1) izpolnjena, potem je obremenitev T 2 gre gor, če je izpolnjena neenakost (2), pa navzdol. Če torej ni izpolnjen noben od teh pogojev, tj.
Torej, če je neenakost (1) izpolnjena, potem je obremenitev T 2 gre gor, če je izpolnjena neenakost (2), pa navzdol. Če torej ni izpolnjen noben od teh pogojev, tj.
![]() ,
,
sistem je negiben.
Še vedno je treba najti silo pritiska na os bloka (slika 14.9). Sila pritiska na os bloka R v tem primeru je mogoče najti kot diagonalo romba ABCD. Ker
Ð ADC= 180° – 2,
kjer je b = 90°– a, potem po kosinusnem izreku
R 2 = .
Od tod ![]() .
.
Odgovori:
1) če ![]() , To
, To ![]() ,
, ![]() ;
;
2) če ![]() , To
, To ![]() , ;
, ;
3) če ![]() , To A = 0; T = T 2 g.
, To A = 0; T = T 2 g.
V vseh primerih ![]() .
.
STOP! Odločite se sami: B13, B15.
Problem 14.4. Na tehtanju vozička M deluje horizontalna sila F(Sl. 14.10, A). Koeficient trenja med obremenitvijo T in voziček je enak m. Določite pospešek bremen. Kakšna naj bo minimalna sila F 0 za nalaganje T začel drseti po vozičku?
| M, T F m |
 A) A)
|  b) riž. 14.10 b) riž. 14.10 |
| A 1 = ? A 2 = ? F 0 = ? | ||
rešitev. Najprej upoštevajte, da sila, ki poganja breme T v gibanju je sila statičnega trenja, s katero voziček deluje na breme. Največja možna vrednost te sile je m mg.
Po tretjem Newtonovem zakonu obremenitev deluje na voziček z enako silo - (slika 14.10, b). Zdrs se začne v trenutku, ko že doseže največjo vrednost, vendar se sistem še vedno giblje kot eno masno telo T+M s pospeškom. Potem po drugem Newtonovem zakonu
Kljub različnim pogojem gibanja se rešitev problema 8 bistveno ne razlikuje od rešitve problema 7. Razlika je le v tem, da pri nalogi 8 sile, ki delujejo na telo, ne ležijo vzdolž ene premice, zato morajo biti projekcije posneto na dveh oseh.
Naloga 8. Konj vleče sani, ki tehtajo 230 kg, nanj deluje s silo 250 N. Koliko bodo sani prevozile, preden dosežejo hitrost 5,5 m/s, ko se premikajo iz mirovanja. Koeficient drsnega trenja sani na snegu je 0,1, gredi pa se nahajajo pod kotom 20° glede na obzorje.
Na sani delujejo štiri sile: vlečna (natezna) sila, usmerjena pod kotom 20° na vodoravno ravnino; gravitacija usmerjena navpično navzdol (vedno); sila reakcije podpore, usmerjena pravokotno na oporo od nje, to je navpično navzgor (v tem problemu); sila drsnega trenja, usmerjena proti gibanju. Ker se bodo sani premikale translatorno, se lahko vse uporabljene sile prenesejo vzporedno na eno točko - na center maše gibljivo telo (sani). Skozi isto točko bomo narisali tudi koordinatne osi (slika 8).
Na podlagi drugega Newtonovega zakona zapišemo enačbo gibanja:
 .
.
Usmerimo os Ox vodoravno vzdolž smeri gibanja (glej sliko 8) in osi Oj– navpično navzgor. Vzemimo projekcije vektorjev, vključenih v enačbo, na koordinatne osi, dodamo izraz za silo drsnega trenja in dobimo sistem enačb:

Rešimo sistem enačb. (Shema za reševanje sistema enačb, ki je podoben sistemu, je običajno enaka: reakcijsko silo opore izrazimo iz druge enačbe in jo nadomestimo v tretjo enačbo, nato pa izraz za silo trenja nadomestimo v prvo enačbo. ) Kot rezultat dobimo:
Preuredimo člene v formuli in delimo njeno desno in levo stran z maso:
 .
.
Ker pospešek ni odvisen od časa, izberemo formulo za kinematiko enakomerno pospešenega gibanja, ki vsebuje hitrost, pospešek in premik:
 .
.
Glede na to, da je začetna hitrost enaka nič, skalarni produkt enako usmerjenih vektorjev pa je enak produktu njihovih modulov, nadomestimo pospešek in izrazimo modul premika:
 ;
;

Dobljena vrednost je odgovor na problem, saj med premočrtnim gibanjem prevožena razdalja in modul premika sovpadata.
Odgovori: sani bodo prevozile 195 m.
Gibanje po nagnjeni ravnini
Opis gibanja majhnih teles po nagnjeni ravnini se bistveno ne razlikuje od opisa gibanja teles navpično in vodoravno, zato je pri reševanju problemov te vrste gibanja, kot v nalogah 7, 8, potrebno tudi zapisati enačbo gibanja in projekcije vektorjev na koordinatne osi. Pri analizi rešitve problema 9 je treba biti pozoren na podobnost pristopa k opisovanju različnih vrst gibanja in na nianse, po katerih se rešitev te vrste problema razlikuje od rešitve zgoraj obravnavanih problemov.
Naloga 9. Smučar drsi po dolgem, ravnem zasneženem hribu, naklonski kot proti obzorju je 30°, dolžina pa 140 m. Kako dolgo bo trajal spust, če je koeficient drsnega trenja smuči na sipkem snegu 0,21 ?

|
podano:
|
rešitev. |
|
|
Gibanje smučarja vzdolž nagnjene ravnine poteka pod vplivom treh sil: gravitacijske sile, usmerjene navpično navzdol; sila reakcije podpore, usmerjena pravokotno na oporo; sila drsnega trenja, usmerjena proti gibanju telesa. Zanemarjanje velikosti smučarja v primerjavi z dolžino drče, Na podlagi drugega Newtonovega zakona zapišemo enačbo gibanja smučar:
 .
.
Izberimo os Ox navzdol vzdolž nagnjene ravnine (slika 9) in osi Oj– pravokotno na nagnjeno ravnino navzgor. Vzemimo projekcije vektorjev enačb na izbrane koordinatne osi, pri čemer upoštevamo, da je pospešek usmerjen navzdol po nagnjeni ravnini, in jim dodamo izraz, ki določa silo drsnega trenja. Dobimo sistem enačb:

Rešimo sistem enačb za pospešek. Da bi to naredili, iz druge enačbe sistema izrazimo reakcijsko silo nosilca in dobljeno formulo nadomestimo v tretjo enačbo, izraz za silo trenja pa v prvo. Po zmanjšanju mase imamo formulo:
 .
.
Pospešek ni odvisen od časa, kar pomeni, da lahko uporabimo formulo za kinematiko enakomerno pospešenega gibanja, ki vsebuje premik, pospešek in čas:
 .
.
Ob upoštevanju dejstva, da je začetna hitrost smučarja enaka nič, modul odmika pa je enak dolžini zdrsa, izrazimo čas iz formule in z nadomestitvijo pospeška v nastalo formulo dobimo:
 ;
;
Odgovori: čas sestopa z gore 9,5 s.