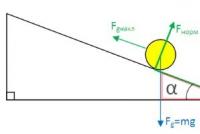
Telo na nagnjeni ravnini. Nagnjena ravnina. Nagnjena ravnina in sile, ki delujejo na telo, ki se nahaja na njej

V našem primeru F n = m g, Ker površina je vodoravna. Toda normalna sila po velikosti ne sovpada vedno s silo gravitacije.

Normalna sila je sila medsebojnega delovanja med površinami teles v stiku; večja kot je, močnejše je trenje.

Normalna sila in sila trenja sta med seboj sorazmerni:

F tr = μF n

0 < μ < 1 - koeficient trenja, ki označuje hrapavost površin.

Pri μ=0 ni trenja (idealiziran primer)

Ko je μ=1, je največja sila trenja enaka normalni sili.

Sila trenja ni odvisna od površine stika dveh površin (če se njuni masi ne spremenita).

Upoštevajte: Eq. F tr = μF n ni razmerje med vektorji, saj so usmerjeni v različne smeri: normalna sila je pravokotna na površino, sila trenja pa vzporedna.

1. Vrste trenja

Obstajata dve vrsti trenja: statična in kinetično.

Statično trenje (statično trenje) deluje med telesi v stiku, ki med seboj mirujeta. Statično trenje se pojavi na mikroskopski ravni.

Kinetično trenje (drsno trenje) deluje med telesi, ki se dotikajo in se gibljejo relativno drug glede na drugega. Kinetično trenje se kaže na makroskopski ravni.

Statično trenje je pri enakih telesih večje od kinetičnega ali pa je koeficient statičnega trenja večji od koeficienta drsnega trenja.

To verjetno veste iz osebnih izkušenj: omaro je zelo težko premakniti, vendar je premikanje omare veliko lažje. To je razloženo z dejstvom, da med premikanjem površine teles "nimajo časa", da bi se med seboj dotaknile na mikroskopski ravni.

Naloga #1: kakšna sila je potrebna za dvig krogle, ki tehta 1 kg, vzdolž nagnjene ravnine, ki leži pod kotom α = 30° na vodoravno ravnino. Torni koeficient μ = 0,1

Izračunamo komponento gravitacije. Najprej moramo ugotoviti kot med nagnjeno ravnino in gravitacijskim vektorjem. Podoben postopek smo že naredili pri upoštevanju gravitacije. Ampak ponavljanje je mati učenja :)

Gravitacijska sila je usmerjena navpično navzdol. Vsota kotov katerega koli trikotnika je 180°. Razmislite o trikotniku, ki ga tvorijo tri sile: gravitacijski vektor; nagnjena ravnina; osnova ravnine (na sliki je označena z rdečo).

Kot med gravitacijskim vektorjem in vznožjem letala je 90°.
Kot med nagnjeno ravnino in njeno osnovo je α

Zato je preostali kot kot med nagnjeno ravnino in gravitacijskim vektorjem:

180° - 90° - α = 90° - α

Komponente gravitacije vzdolž nagnjene ravnine:

F g naklon = F g cos(90° - α) = mgsinα

Potrebna sila za dvig žoge:

F = F g incl + F trenje = mgsinα + F trenje

Treba je določiti silo trenja F tr. Ob upoštevanju statičnega koeficienta trenja:

Trenje F = μF norma

Izračunajte normalno silo F normalno, ki je enaka komponenti gravitacije, pravokotni na nagnjeno ravnino. Vemo že, da je kot med gravitacijskim vektorjem in nagnjeno ravnino 90° - α.

F norma = mgsin(90° - α) = mgcosα
F = mgsinα + μmgcosα

F = 1 9,8 sin30° + 0,1 1 9,8 cos30° = 4,9 + 0,85 = 5,75 N

Na kroglo bomo morali uporabiti silo 5,75 N, da jo bomo odkotalili do vrha nagnjene ravnine.

Naloga št. 2: določite, kako daleč se bo skotalila krogla z maso m = 1 kg vzdolž vodoravne ravnine, kotaljenje po nagnjeni ravnini dolžine 10 metrov pri koeficientu drsnega trenja μ = 0,05

Sile, ki delujejo na kotalečo se kroglo, so prikazane na sliki.

Gravitacijska komponenta vzdolž nagnjene ravnine:

F g cos(90° - α) = mgsinα

Normalna moč:

F n = mgsin(90° - α) = mgcos(90° - α)

Sila drsnega trenja:

Trenje F = μF n = μmgsin(90° - α) = μmgcosα

Rezultantna sila:

F = F g - F trenje = mgsinα - μmgcosα

F = 1 9,8 sin30° - 0,05 1 9,8 0,87 = 4,5 N

F = ma; a = F/m = 4,5/1 = 4,5 m/s 2

Določite hitrost žogice na koncu nagnjene ravnine:

V 2 = 2as; V = 2as = 2 4,5 10 = 9,5 m/s

Žoga konča gibanje po nagnjeni ravnini in se začne premikati po vodoravni ravnini s hitrostjo 9,5 m/s. Zdaj v vodoravni smeri na kroglico deluje samo sila trenja, komponenta gravitacije pa je enaka nič.

Skupna sila:

F = μF n = μF g = μmg = 0,05 1 9,8 = -0,49 N

Znak minus pomeni, da je sila usmerjena v nasprotno smer od gibanja. Določimo pospešek pojemka žoge:

a = F/m = -0,49/1 = -0,49 m/s 2

Zavorna pot krogle:

V 1 2 - V 0 2 = 2as; s = (V 1 2 - V 0 2)/2a

Ker določamo pot žogice do popolne ustavitve, torej V 1 =0:

s = (-V 0 2)/2a = (-9,5 2)/2·(-0,49) = 92 m

Naša žoga se je premočrtno skotalila kar 92 metrov!

Dinamika je ena izmed pomembnih vej fizike, ki preučuje vzroke gibanja teles v prostoru. V tem članku bomo s teoretičnega vidika obravnavali enega od tipičnih problemov dinamike - gibanje telesa vzdolž nagnjene ravnine, in podali tudi primere rešitev nekaterih praktičnih problemov.

Osnovna formula dinamike

Preden preidemo na študij fizike gibanja telesa vzdolž nagnjene ravnine, predstavimo potrebne teoretične informacije za rešitev tega problema.

V 17. stoletju je Isaac Newton, zahvaljujoč praktičnim opazovanjem gibanja makroskopskih okoliških teles, izpeljal tri zakone, ki danes nosijo njegovo ime. Vsa klasična mehanika temelji na teh zakonih. Ta člen nas zanima samo v drugem zakonu. Njegova matematična oblika je podana spodaj:

Formula pravi, da bo delovanje zunanje sile F¯ posredovalo telesu z maso m pospešek a¯. Ta preprost izraz bomo nadalje uporabili za reševanje problemov gibanja telesa vzdolž nagnjene ravnine.

Upoštevajte, da sta sila in pospešek vektorski količini, usmerjeni v isto smer. Poleg tega je sila aditivna značilnost, kar pomeni, da je v zgornji formuli F¯ mogoče obravnavati kot posledični učinek na telo.

Nagnjena ravnina in sile, ki delujejo na telo, ki se nahaja na njej

Ključna točka, od katere je odvisen uspeh reševanja problemov gibanja telesa vzdolž nagnjene ravnine, je določitev sil, ki delujejo na telo. Opredelitev sil razumemo kot poznavanje njihovih modulov in smeri delovanja.

Spodaj je risba, ki prikazuje, da telo (avto) miruje na ravnini, ki je nagnjena pod kotom na vodoravno ravnino. Katere sile delujejo nanj?

Spodnji seznam navaja te sile:

• težnost;
• podporne reakcije;
• trenje;
• napetost niti (če obstaja).

Gravitacija

Najprej je to sila gravitacije (F g). Usmerjen je navpično navzdol. Ker ima telo sposobnost gibanja samo po površini ravnine, se pri reševanju nalog gravitacijska sila razgradi na dve medsebojno pravokotni komponenti. Ena od komponent je usmerjena vzdolž ravnine, druga je pravokotna nanjo. Samo prvi od njih vodi do pojava pospeška v telesu in je pravzaprav edini gonilni dejavnik zadevnega telesa. Druga komponenta določa pojav reakcijske sile podpore.

Reakcija tal

Druga sila, ki deluje na telo, je reakcija tal (N). Razlog za njegov pojav je povezan s tretjim Newtonovim zakonom. Vrednost N prikazuje silo, s katero ravnina deluje na telo. Usmerjen je navzgor pravokotno na nagnjeno ravnino. Če bi bilo telo na vodoravni površini, bi bil N enak njegovi teži. V obravnavanem primeru je N enak le drugi komponenti, dobljeni z raztezanjem gravitacije (glej odstavek zgoraj).

Reakcija podpore nima neposrednega vpliva na naravo gibanja telesa, saj je pravokotna na ravnino naklona. Kljub temu povzroča trenje med telesom in površino letala.

Sila trenja

Tretja sila, ki jo moramo upoštevati pri proučevanju gibanja telesa po nagnjeni ravnini, je trenje (F f). Fizična narava trenja je kompleksna. Njegov pojav je povezan z mikroskopskimi interakcijami kontaktnih teles z nehomogenimi kontaktnimi površinami. Obstajajo tri vrste te sile:

• mir;
• zdrs;
• valjanje.

Statično in drsno trenje opisuje ista formula:

kjer je µ brezdimenzijski koeficient, katerega vrednost je določena z materiali drgnih teles. Torej, z drsnim trenjem lesa na lesu, µ = 0,4, in ledu na ledu - 0,03. Koeficient statičnega trenja je vedno večji od koeficienta drsenja.

Kotalno trenje opisujemo z drugačno formulo od prejšnje. Izgleda:

Tukaj je r polmer kolesa, f je koeficient, ki ima dimenzijo inverzne dolžine. Ta sila trenja je običajno veliko manjša od prejšnjih. Upoštevajte, da na njegovo vrednost vpliva polmer kolesa.

Sila F f, ne glede na vrsto, je vedno usmerjena proti gibanju telesa, to pomeni, da F f teži, da telo ustavi.

Napetost niti

Pri reševanju problemov gibanja telesa po nagnjeni ravnini ta sila ni vedno prisotna. Njegov videz določa dejstvo, da je telo, ki se nahaja na nagnjeni ravnini, povezano z drugim telesom z neraztegljivo nitjo. Pogosto drugo telo visi na nitki skozi blok zunaj ravnine.

Na predmet, ki se nahaja na ravnini, deluje natezna sila niti, ki jo pospešuje ali upočasnjuje. Vse je odvisno od velikosti sil, ki delujejo v fizičnem sistemu.

Pojav te sile v problemu bistveno oteži postopek reševanja, saj je treba hkrati upoštevati gibanje dveh teles (na ravnini in visi).

Problem določanja kritičnega kota

Zdaj je prišel čas, da opisano teorijo uporabimo za reševanje realnih problemov gibanja vzdolž nagnjene ravnine telesa.

Predpostavimo, da ima lesen tram maso 2 kg. Je na leseni letali. Treba je ugotoviti, pri katerem kritičnem kotu naklona ravnine bo žarek začel drseti vzdolž nje.

Drsenje žarka se bo zgodilo le, če bo skupna sila, ki deluje navzdol vzdolž ravnine nanj, večja od nič. Tako je za rešitev tega problema dovolj določiti posledično silo in najti kot, pri katerem postane večji od nič. V skladu s pogoji problema bosta na žarek vzdolž ravnine delovali le dve sili:

• gravitacijska komponenta F g1 ;
• statično trenje F f .

Da telo začne drseti, mora biti izpolnjen naslednji pogoj:

Upoštevajte, da če komponenta gravitacije presega statično trenje, bo tudi večja od sile drsnega trenja, to pomeni, da se bo začeto gibanje nadaljevalo s stalnim pospeškom.

Spodnja slika prikazuje smeri vseh delujočih sil.

Označimo kritični kot s simbolom θ. Enostavno je pokazati, da bosta sili F g1 in F f enaki:

F g1 = m × g × sin(θ);

F f = µ × m × g × cos(θ).

Tukaj je m × g teža telesa, µ je koeficient statične sile trenja za par materialov les-les. Iz ustrezne tabele koeficientov lahko ugotovite, da je enak 0,7.

Če zamenjamo najdene vrednosti v neenakost, dobimo:

m × g × sin(θ) ≥ µ × m × g × cos(θ).

S pretvorbo te enakosti pridemo do pogoja gibanja telesa:

tan(θ) ≥ µ =>

θ ≥ arctan(µ).

Dobili smo zelo zanimiv rezultat. Izkazalo se je, da vrednost kritičnega kota θ ni odvisna od mase telesa na nagnjeni ravnini, ampak je enolično določena s koeficientom statičnega trenja µ. Če njegovo vrednost zamenjamo v neenakost, dobimo vrednost kritičnega kota:

θ ≥ arctan(0,7) ≈ 35 o .

Naloga določanja pospeška pri gibanju vzdolž nagnjene ravnine telesa

Zdaj pa rešimo malo drugačen problem. Naj bo lesen tram na stekleni nagnjeni ravnini. Letalo je nagnjeno pod kotom 45 o proti obzorju. Ugotoviti je treba, s kakšnim pospeškom se bo gibalo telo, če je njegova masa 1 kg.

Zapišimo glavno enačbo dinamike za ta primer. Ker bo sila F g1 usmerjena vzdolž gibanja, F f pa proti njej, bo enačba v obliki:

F g1 - F f = m × a.

Nadomestimo formule, dobljene v prejšnjem problemu za sili F g1 in F f, imamo:

m × g × sin(θ) - µ × m × g × cos(θ) = m × a.

Kje dobimo formulo za pospešek:

a = g × (sin(θ) - µ × cos(θ)).

Spet imamo formulo, ki ne vključuje telesne teže. To dejstvo pomeni, da bodo bloki katere koli mase istočasno zdrsnili navzdol po nagnjeni ravnini.

Glede na to, da je koeficient µ za drgne materiale les-steklo 0,2, nadomestimo vse parametre v enačbo in dobimo odgovor:

Tako je tehnika za reševanje problemov z nagnjeno ravnino določitev rezultantne sile, ki deluje na telo, in nato uporaba drugega Newtonovega zakona.

Fizika: gibanje telesa po nagnjeni ravnini. Primeri rešitev in problemov - vse zanimivosti in dosežki znanosti in izobraževanja na spletnem mestu

Na nagnjeni ravnini, dolgi 13 m in visoki 5 m, leži masa 26 kg. Koeficient trenja je 0,5. S kakšno silo je treba delovati na breme vzdolž ravnine, da se breme vleče? ukrasti tovor
REŠITEV

S kakšno silo je treba dvigniti voziček, ki tehta 600 kg, po nadvozu z naklonom 20°, če je koeficient upora gibanja 0,05
REŠITEV

Med laboratorijskim delom smo pridobili naslednje podatke: dolžina nagnjene ravnine je 1 m, višina 20 cm, masa lesenega bloka je 200 g, vlečna sila, ko se blok premika navzgor, je 1 N. Poiščite koeficient trenja
REŠITEV

Blok z maso 2 kg leži na nagnjeni ravnini, dolgi 50 cm in visoki 10 cm. Z dinamometrom, nameščenim vzporedno z ravnino, so blok najprej potegnili navzgor po nagnjeni ravnini in nato potegnili navzdol. Poiščite razliko v odčitkih na dinamometru
REŠITEV

Za držanje vozička na nagnjeni ravnini s kotom naklona α je potrebno uporabiti silo F1, usmerjeno navzgor vzdolž nagnjene ravnine, za dvig navzgor pa uporabiti silo F2. Poiščite koeficient upora
REŠITEV

Nagnjena ravnina leži pod kotom α = 30° glede na vodoravno ravnino. Pri katerih vrednostih koeficienta trenja μ je težje potegniti breme vzdolž njega kot ga dvigniti navpično?
REŠITEV

Na nagnjeni ravnini, dolgi 5 m in visoki 3 m, je masa 50 kg. Kakšna sila, usmerjena vzdolž ravnine, mora delovati, da zadrži to obremenitev? enakomerno potegnite gor? vleče s pospeškom 1 m/s2? Koeficient trenja 0,2
REŠITEV

Avto, ki tehta 4 tone, se giblje navkreber s pospeškom 0,2 m/s2. Poiščite vlečno silo, če je naklon 0,02 in koeficient upora 0,04
REŠITEV

Vlak, ki tehta 3000 ton, se premika po klancu navzdol 0,003. Koeficient upora gibanja je 0,008. S kolikšnim pospeškom se premika vlak, če je vlečna sila lokomotive: a) 300 kN; b) 150 kN; c) 90 kN
REŠITEV

Motorno kolo z maso 300 kg se je začelo premikati iz mirovanja na vodoravnem odseku ceste. Nato je šla cesta navzdol, enako 0,02. Kolikšno hitrost je dosegel motocikel 10 sekund po začetku premikanja, če je vodoravni odsek ceste v tem času prevozil polovično? Vlečna sila in koeficient upora gibanja sta konstantna na celotni poti in sta enaka 180 N oziroma 0,04
REŠITEV

Blok z maso 2 kg je postavljen na nagnjeno ravnino z naklonskim kotom 30°. Kakšna sila, usmerjena vodoravno (slika 39), mora delovati na blok, da se enakomerno premika vzdolž nagnjene ravnine? Koeficient trenja med blokom in nagnjeno ravnino je 0,3
REŠITEV

Na ravnilo položite majhen predmet (gumijasti trak, kovanec itd.). Postopoma dvigujte konec ravnila, dokler predmet ne začne drseti. Izmerite višino h in osnovo b nastale nagnjene ravnine in izračunajte koeficient trenja
REŠITEV

S kakšnim pospeškom a drsi kvader po nagnjeni ravnini z naklonskim kotom α = 30° s koeficientom trenja μ = 0,2
REŠITEV

V trenutku, ko je prvo telo začelo prosto padati z določene višine h, je drugo telo začelo brez trenja drseti z nagnjene ravnine enake višine h in dolžine l = nh. Primerjaj končne hitrosti teles na dnu nagnjene ravnine in čas njihovega gibanja.

Premikanje. Toplota Kitaygorodsky Alexander Isaakovič

Nagnjena ravnina

Nagnjena ravnina

Strm vzpon je težje premagati kot položen. Telo je lažje kotaliti po nagnjeni ravnini kot dvigniti navpično. Zakaj je to in koliko lažje? Zakon dodajanja sil nam omogoča razumevanje teh vprašanj.

Na sl. Slika 12 prikazuje voziček na kolesih, ki ga na nagnjeni ravnini drži napetost vrvi. Na voziček poleg vlečne sile delujeta še dve sili - teža in sila reakcije opore, ki vedno deluje normalno na podlago, ne glede na to, ali je površina opore vodoravna ali nagnjena.

Kot smo že omenili, če telo pritisne na oporo, se opora upira pritisku ali, kot pravijo, ustvarja reakcijsko silo.

Zanima nas, v kolikšni meri je lažje vleči voziček po nagnjeni ravnini navzgor kot ga dvigniti navpično.

Razporedimo sile tako, da je ena usmerjena vzdolž, druga pa pravokotno na površino, po kateri se telo giblje. Da telo počiva na nagnjeni ravnini, mora natezna sila vrvi uravnotežiti le vzdolžno komponento. Kar zadeva drugo komponento, je uravnotežena z reakcijo podpore.

Poiščite silo napetosti vrvi, ki nas zanima T To lahko naredimo z geometrijsko konstrukcijo ali s trigonometrijo. Geometrična konstrukcija je sestavljena iz risanja s konca vektorja teže p pravokotno na ravnino.

Na sliki lahko najdete dva podobna trikotnika. Razmerje dolžine nagnjene ravnine l do višine h enaka razmerju ustreznih stranic v trikotniku sil. Torej,

Bolj ko je nagnjena ravnina ( h/l majhna), lažje je seveda povleči telo navzgor.

Zdaj pa za poznavalce trigonometrije: saj je kot med prečno komponento uteži in vektorjem teže enak kotu? nagnjena ravnina (to so koti z med seboj pravokotnima stranicama), tedaj

Torej, zakotalite voziček po nagnjeni ravnini pod kotom? v grehu? krat lažje kot dvigovanje navpično.

Koristno si je zapomniti vrednosti trigonometričnih funkcij za kote 30, 45 in 60°. Če poznamo te številke za sinus (sin 30° = 1/2; sin 45° = sqrt(2)/2;*5 sin 60° = sqrt(3)/2), bomo dobili dobro predstavo o dobitku v veljavi pri premikanju vzdolž nagnjene ravnine.

Iz formul je razvidno, da bodo s kotom nagnjene ravnine 30 ° naša prizadevanja polovična teža: T = p·(1/2). Pri kotih 45° in 60° boste morali vrv vleči s silami, ki so približno enake 0,7 in 0,9 teže vozička. Kot lahko vidite, tako strme nagnjene ravnine stvari ne olajšajo veliko.

Naj se telo, ki se lahko vrti (na primer valj), kotali po nagnjeni ravnini. Predvidevamo, da med gibanjem ne pride do zdrsa. To pomeni, da je hitrost telesa na dotični točki A enako nič. Odsotnost drsenja je zagotovljena z delovanjem sil iz nagnjene ravnine. Na telo, ki se vrti, delujejo: gravitacija, normalna sila reakcije tal in sila trenja
(slika 1.5). Vektorji teh sil na sliki so prikazani tako, da izhajajo iz njihovih delovnih točk. V odsotnosti drsenja sila trenja
je sila statičnega trenja ali sila adhezijskega trenja.

.

V skalarni obliki glede na os X, usmerjen vzdolž ravnine navzdol, ima ta enačba obliko:

Vrtenje telesa okoli osi, ki poteka skozi središče mase Z, povzroča samo sila trenja, saj so momenti sil normalne reakcije podpore in gravitacije enaki nič, saj potekajo črte delovanja teh sil skozi vrtilno os. Zato ima enačba za dinamiko rotacijskega gibanja obliko:

,

Kje jaz– vztrajnostni moment telesa,
– kotni pospešek, r– polmer telesa,
– moment sile trenja. Zato:

(1.11)

Iz izrazov (1.10) in (1.11) imamo:

(1.12)

Za gibanje valja po nagnjeni ravnini uporabimo zakon o ohranitvi energije. Kinetična energija rotirajočega telesa je enaka vsoti kinetične energije translacijskega gibanja središča mase tega telesa in rotacijskega gibanja točk telesa glede na os, ki poteka skozi središče mase:

, (1.13)

kjer je ω kotna hitrost, ki je povezana s hitrostjo središča mase z razmerjem:

. (1.14)

V odsotnosti drsenja deluje sila trenja na tiste točke telesa, ki ležijo na trenutni osi vrtenja. A. Trenutna hitrost takih točk je enaka nič in se zato uporablja zanje sila trenja sklopke ne proizvaja dela in ne vpliva na vrednost celotne kinetične energije kotalnega telesa. Vloga trenja sklopke gre za vrtenje telesa in zagotavljanje čistega kotaljenja. V prisotnosti trenja sklopke gre gravitacijsko delo za povečanje kinetične energije ne le translacijskega, temveč tudi rotacijskega gibanja telesa. Posledično bo zakon o ohranitvi energije telesa, ki se kotali po nagnjeni ravnini, zapisan v obliki:

, (1.15)

kje je kinetična energija E Za je določena s formulo (1.13), potencialna energija pa E p = mgh.

2. Opis laboratorijske postavitve

Laboratorijska postavitev (slika 2.1.) je nagnjena ravnina 1, viš h in dolžina l. Zaklepni mehanizem 2 je nameščen na zgornji točki ravnine; na dnu je kontrolni senzor 3, povezan s štoparico 4.

3. Delovni nalog

1. Eksperimentirajte s progresivno premikajočim se telesom

Elektronsko enoto priključite na omrežje z napajalnim kablom.

Postavite telo (palico) v zaklepni mehanizem 2, medtem ko morajo biti odčitki štoparice na nič.

Spustite telo, medtem ko bo zdrsnilo navzdol po nagnjeni ravnini. Ko se telo dotakne kontrolnega senzorja 3, odčitajte podatke s štoparice. Poskus izvedite vsaj petkrat.

Izmerite maso bloka m.

Izmeri dolžino l in višina h nagnjena ravnina.

Podatke vnesite v tabelo 1.

Tabela 1

11. Zapišite zakon o ohranjanju energije za gibljivo telo (1.9), preverite njegovo izpolnitev ob upoštevanju sile trenja za povprečne vrednosti ,,
. Navedite natančnost izpolnjevanja tega zakona v odstotkih.